4.2 splitbit.h
The split_bit function is declared in the header file. First it will take three arguments; first the value to split (int value), where to start the split(start), where to stop(int end ). Example: to split dec’10’ from bit 3 down to 1. Then value=10, start=3, end=1.
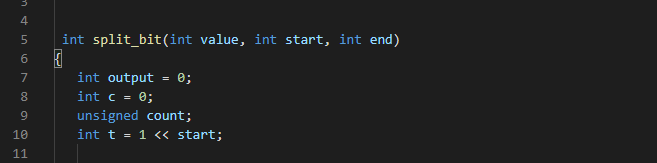
4.3 splitbit.c
First we include splitbit.h
We create four integer variables.
int output-(Final output after split),
int C -(Intermediate signal),
unsigned count-(will be used in for loop),
t = 1<<start In our case t = 1<<3 = 1000.
note:1 shifting a bit to the left is equivalent to multiplying by two while shifting to the right is equivalent to dividing by two.
note:2 In the case of binary values preceded with zeros. Dividing by 2 means removing one zero from the right and multiplying by 2 means adding zero to the left. Example: binary’1000’ / 2 == binary’1000’ >> 1 ==100. binary’1000’ x 2 = binary’1000’ << 1 = 10000. This holds true for binary values.
Next, we create a for loop that loops through count = 1<<15 down to 0.1, and each step reducing by 0 or dividing by two, comparing its value with our
value. Example: dec’10’ = binary’0000 0000 0000 1010’. Our for loop starts from count = 1<<15 = binary’1000 0000 0000 0000’. And keeps reducing by 0. This loops the ‘1’ at bit 15 downto 14 and continues to reduce. At each step it compares it with our dec’10’. It will be false until it gets to bit 3 and bit 1 where both our dec’10’ and count are equal to 1.
At bit 3 and bit 1 another if statement also checks if it has less than or equal to our start bit. In our case, the start bit, t= 1<<start = 1<< 3 = 1000. What this if statement block does is to make sure we take into account only starting from the start bit, any value above the start is discarded. In our case, if our decimal value and our count is equal to one from bit 15 downto 4, it is ignored.
Next step above, is to divide it by our end bit. What this does is that it changes the position of the original bit. In our case bit3(1000) >> end bit(1), and bit1(10) >> end bit(1). Will now become binary’100’ and binary’1’ respectively. On line 16, The output serves as an accumulator which adds them up.
output = binary’100 + 1’ = bin’101’ = dec’5’. So, bit 3 down to 1 of dec’10’ = 5.
The above function is based on the binary position of decimal integers. This function will be used throughout this course to split bits and select certain parts of the bits. Given the value, start, and end.