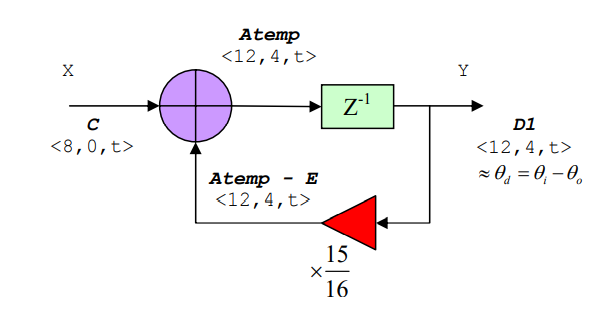
Numerical Controlled Oscillator
Numerical Controlled Oscillator (NCO) will take the corrective error voltage, Vd(n) and then shift its output frequency from its free-running value to the
input signal frequency ωi and thus keep the PLL in lock. The block diagram can be seen below
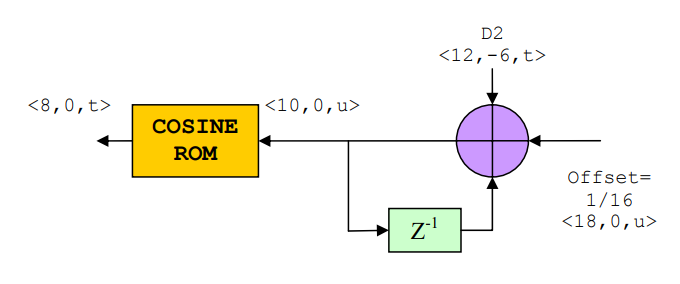
Here we assume the NCO free running frequency is 1 MHz and the system clock frequency is 16 MHz; there are 16 sampling points in one cycle of 1 MHz free running frequency. When input is zero, NCO has to generate output equal to free running frequency. Since there are 16 sampling points in one cycle of free running frequency, so the offset must be 1/16. The greater input will produce greater frequency, and vice versa.
Here we assume the NCO free running frequency is 1 MHz and the system clock frequency is 16 MHz; there are 16 sampling points in one cycle of 1 MHz free running frequency. When input is zero, NCO has to generate output equal to free running frequency. Since there are 16 sampling points in one cycle of free running frequency, so the offset must be 1/16. The greater input will produce greater frequency, and vice versa.
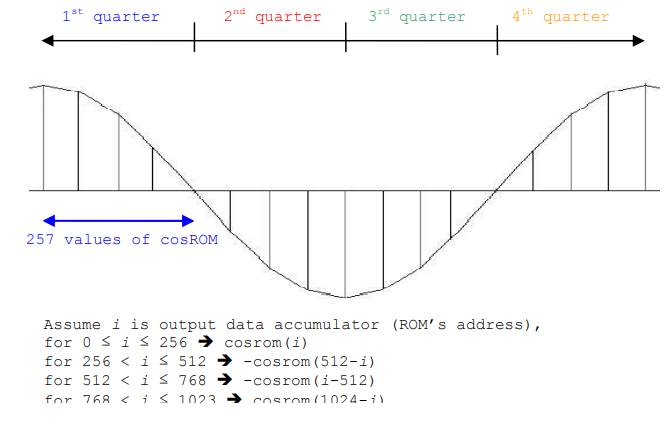
The system is a simple integrator which accumulates the input value and maps it into predefined cosine ROM. All 1024 values were given (file: cos.txt) to define one cycle of cosine signal, but we actually don’t need to use all of these values. Since one cycle can be divided to four quarter, we only need to define the first quarter with 257 values. The remains quarters are duplicated form the first quarter, where the opposite sign is applied to second and third quarter. Illustration is shown above
LIBRARY ieee; USE ieee.std_logic_1164.all; USE IEEE.numeric_std.ALL; ENTITY nco IS -- Declarations port ( clk : in std_logic; reset : in std_logic; din : in signed(11 downto 0); dout : out signed(7 downto 0) ); END nco ; -- hds interface_end ARCHITECTURE behavior OF nco IS type vectype is array (0 to 256) of signed(7 downto 0); -- ROM cosrom constant cosrom : vectype := ( 0 => "01111111", 1 => "01111111", 2 => "01111111", 3 => "01111111", 4 => "01111111", 5 => "01111111", 6 => "01111111", 7 => "01111111", 8 => "01111111", 9 => "01111111", 10 => "01111111", 11 => "01111111", 12 => "01111111", 13 => "01111111", 14 => "01111111", 15 => "01111111", 16 => "01111111", 17 => "01111111", 18 => "01111111", 19 => "01111111", 20 => "01111111", 21 => "01111111", 22 => "01111111", 23 => "01111111", 24 => "01111111", 25 => "01111110", 26 => "01111110", 27 => "01111110", 28 => "01111110", 29 => "01111110", 30 => "01111110", 31 => "01111110", 32 => "01111110", 33 => "01111101", 34 => "01111101", 35 => "01111101", 36 => "01111101", 37 => "01111101", 38 => "01111101", 39 => "01111100", 40 => "01111100", 41 => "01111100", 42 => "01111100", 43 => "01111100", 44 => "01111011", 45 => "01111011", 46 => "01111011", 47 => "01111011", 48 => "01111010", 49 => "01111010", 50 => "01111010", 51 => "01111010", 52 => "01111010", 53 => "01111001", 54 => "01111001", 55 => "01111001", 56 => "01111001", 57 => "01111000", 58 => "01111000", 59 => "01111000", 60 => "01110111", 61 => "01110111", 62 => "01110111", 63 => "01110111", 64 => "01110110", 65 => "01110110", 66 => "01110110", 67 => "01110101", 68 => "01110101", 69 => "01110101", 70 => "01110100", 71 => "01110100", 72 => "01110100", 73 => "01110011", 74 => "01110011", 75 => "01110011", 76 => "01110010", 77 => "01110010", 78 => "01110010", 79 => "01110001", 80 => "01110001", 81 => "01110001", 82 => "01110000", 83 => "01110000", 84 => "01101111", 85 => "01101111", 86 => "01101111", 87 => "01101110", 88 => "01101110", 89 => "01101101", 90 => "01101101", 91 => "01101101", 92 => "01101100", 93 => "01101100", 94 => "01101011", 95 => "01101011", 96 => "01101010", 97 => "01101010", 98 => "01101010", 99 => "01101001", 100 => "01101001", 101 => "01101000", 102 => "01101000", 103 => "01100111", 104 => "01100111", 105 => "01100110", 106 => "01100110", 107 => "01100101", 108 => "01100101", 109 => "01100100", 110 => "01100100", 111 => "01100011", 112 => "01100011", 113 => "01100010", 114 => "01100010", 115 => "01100001", 116 => "01100001", 117 => "01100000", 118 => "01100000", 119 => "01011111", 120 => "01011111", 121 => "01011110", 122 => "01011110", 123 => "01011101", 124 => "01011101", 125 => "01011100", 126 => "01011100", 127 => "01011011", 128 => "01011011", 129 => "01011010", 130 => "01011001", 131 => "01011001", 132 => "01011000", 133 => "01011000", 134 => "01010111", 135 => "01010111", 136 => "01010110", 137 => "01010101", 138 => "01010101", 139 => "01010100", 140 => "01010100", 141 => "01010011", 142 => "01010010", 143 => "01010010", 144 => "01010001", 145 => "01010001", 146 => "01010000", 147 => "01001111", 148 => "01001111", 149 => "01001110", 150 => "01001110", 151 => "01001101", 152 => "01001100", 153 => "01001100", 154 => "01001011", 155 => "01001010", 156 => "01001010", 157 => "01001001", 158 => "01001000", 159 => "01001000", 160 => "01000111", 161 => "01000111", 162 => "01000110", 163 => "01000101", 164 => "01000101", 165 => "01000100", 166 => "01000011", 167 => "01000011", 168 => "01000010", 169 => "01000001", 170 => "01000001", 171 => "01000000", 172 => "00111111", 173 => "00111110", 174 => "00111110", 175 => "00111101", 176 => "00111100", 177 => "00111100", 178 => "00111011", 179 => "00111010", 180 => "00111010", 181 => "00111001", 182 => "00111000", 183 => "00111000", 184 => "00110111", 185 => "00110110", 186 => "00110101", 187 => "00110101", 188 => "00110100", 189 => "00110011", 190 => "00110011", 191 => "00110010", 192 => "00110001", 193 => "00110000", 194 => "00110000", 195 => "00101111", 196 => "00101110", 197 => "00101101", 198 => "00101101", 199 => "00101100", 200 => "00101011", 201 => "00101010", 202 => "00101010", 203 => "00101001", 204 => "00101000", 205 => "00100111", 206 => "00100111", 207 => "00100110", 208 => "00100101", 209 => "00100100", 210 => "00100100", 211 => "00100011", 212 => "00100010", 213 => "00100001", 214 => "00100001", 215 => "00100000", 216 => "00011111", 217 => "00011110", 218 => "00011110", 219 => "00011101", 220 => "00011100", 221 => "00011011", 222 => "00011011", 223 => "00011010", 224 => "00011001", 225 => "00011000", 226 => "00011000", 227 => "00010111", 228 => "00010110", 229 => "00010101", 230 => "00010100", 231 => "00010100", 232 => "00010011", 233 => "00010010", 234 => "00010001", 235 => "00010001", 236 => "00010000", 237 => "00001111", 238 => "00001110", 239 => "00001101", 240 => "00001101", 241 => "00001100", 242 => "00001011", 243 => "00001010", 244 => "00001010", 245 => "00001001", 246 => "00001000", 247 => "00000111", 248 => "00000110", 249 => "00000110", 250 => "00000101", 251 => "00000100", 252 => "00000011", 253 => "00000010", 254 => "00000010", 255 => "00000001", 256 => "00000000"); signal dtemp : unsigned(17 downto 0); signal din_buf : signed(17 downto 0); signal dtemp1 : integer; constant offset : unsigned(17 downto 0) := "000100000000000000"; begin process(CLK, RESET) begin if (RESET='1') then dout <= (others => '0'); din_buf <= (others => '0'); dtemp <= (others => '0'); dtemp1 <= 0; elsif rising_edge(CLK) then din_buf <= din(11)&din(11)&din(11)&din(11)&din(11)&din(11)&din; dtemp <= dtemp + unsigned(din_buf) + offset; dtemp1 <= to_integer(dtemp(17 downto 8)); if (dtemp1 >= 0) and (dtemp1 < 257) then dout <= cosrom(dtemp1); elsif (dtemp1 >= 257) and (dtemp1 < 513) then dout <= -cosrom(512-dtemp1); elsif (dtemp1 >= 513) and (dtemp1 < 769) then dout <= -cosrom(dtemp1-512); else dout <= cosrom(1024-dtemp1); end if; end if; end process; END behavior;