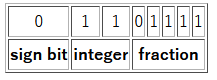
In this chapter we are going to design a digital FM receiver circuit, assuming the Frequency Modulated signal is converted to series of numerical values (digital signal) via Analog to Digital Conversion (ADC) circuit. CREDIT TO THE ORIGINAL OWNER Nursani Rahmatullah(Institute of technology Bandung).
The design of the Digital FM Receiver circuit in this project uses Phase Locked Loop (PLL) as the main core. The task of the PLL is to maintain coherence between the input (modulated) signal frequency, ωi and the respective output frequency, ωo via phase comparison. This self-correcting ability of the system also allows the PLL to track the frequency changes of the input signal once it is locked. Frequency modulated input signal is assumed as a series of numerical values (digital signal) via 8-bit of analog to digital conversion (ADC) circuit. The FM Receiver gets the 8 bits signal every clock cycle and outputs the demodulated signal.

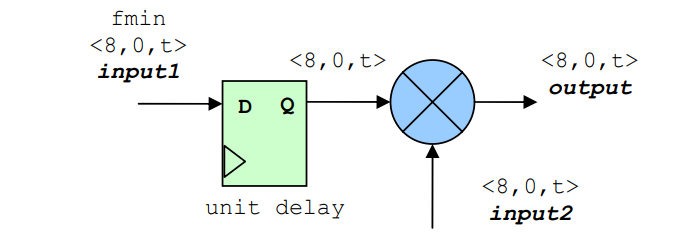
Phase Detector (PD) detects phase error between input signal and output signal from NCO(Numerical controlled Oscillator we discuss this later section). This operation employs a multiplier module as shown below. The input signal is frequency modulated, so the input signal Vi(n) can be expressed as follows:
Vi(n) = sin( ωi(n)+ θi)
Feedback loop mechanism of the PLL will force NCO to generate sinusoidal signal Vo(n) with the same frequency of Vi(n), then:
Vo(n) = cos(ωi(n) + θo)
Output of phase detector is product of these two signals, using familiar trigonometric identity we obtain:
Vd(n) =Kdsin(ωi(n) + θi) cos(ωi(n) + θo)
Kd/2[sin(2ωin + θi+ θo) + sin( θi - θo)]
Kd is the gain of the phase detector. The first term corresponds to high frequency component. The second term corresponds to the phase difference between Vi(n) and Vo(n) . By removing the first term thru loop filtering, the phase difference can be obtained.
In the VHDL model, we use Booth’s Multiplication algorithm for the multiplier instead of simple signed arithmetic multiplier operation (denoted by ∗ ). Arithmetic multiplier will consume large area, while Booth’s multiplication algorithm for 8-bit multiplication only needs eight 8-bit adders which is much save in area consumption. The Booth’s Multiplication algorithm is discussed below.
A typical implementation of Booth's algorithm
Booth's algorithm can be implemented by repeatedly adding (with ordinary unsigned binary addition) one of two predetermined values A and S to a product P, then performing a
rightward arithmetic shift on P. Let m and r be the multiplicand and multiplier, respectively; and let x and y
represent the number of bits in m and r. The Booth's algorithm steps are given below.
1. Determine the values of A and S, and the initial value of P. All of these numbers should have a length equal to (x + y + 1).
2. Determine the two least significant (rightmost) bits of P.
3. Arithmetically shift the value obtained in the 2nd step by a single place to the right. Let P now equal this new value.
4. Repeat steps 2 and 3 until they have been done y times.
5. Drop the least significant (rightmost) bit from P. This is the product of m and r.
Example
Find 3 × (−4), with m = 3 and r = −4, and x = 4 and y = 4:
Perform the loop four times:
P = 0000 1100 0. The last two bits are 00.
The above-mentioned technique is inadequate when the multiplicand is the most negative number that can be represented (e.g. if the multiplicand has 4 bits then this value is −8). One possible correction to this problem is to add one more bit to the left of A, S and P. This then follows the implementation described above, with modifications in determining the bits of A and S;
e.g., the value of m, originally assigned to the first x bits of A, will be assigned to the first x+1 bits of A. Below, the improved technique is demonstrated by multiplying −8 by 2 using 4 bits for the multiplicand and the multiplier:
This previous example was edited from wiki, now this is our own implementation:
consider y = 1101, x = 1011; where x*y = 10001111 = M. WATCH THE VIDEO FOR EXPLANATION
| Y | X | Description |
|---|---|---|
| 1 | 1-1-1-1-0-1-0-1 | -X |
| 01 | 0-0-0-1-0-1-1 | X |
| 10 | 1-1-0-1-0-1 | -X |
| 11 | 0-0-0-0-0 | 0 |
| 01 | 1-0-1-1 | X |
| sum total | 1-0-0-0-1-1-1-1 | => M |
LIBRARY ieee; USE ieee.std_logic_1164.all; USE IEEE.numeric_std.ALL; ENTITY multiplier IS -- Declarations port (CLK : in std_logic; RESET : in std_logic; input1 : in std_logic_vector(7 downto 0); input2 : in signed(7 downto 0); output : out signed(7 downto 0) ); END multiplier ; ARCHITECTURE behavior OF multiplier IS signal out_temp : signed(15 downto 0); signal input1_buf : signed(15 downto 0); signal part0, part1, part2, part3, part4, part5, part6, part7 : signed(15 downto 0); begin process(CLK, RESET) begin if (RESET='1') then out_temp <= (others => '0'); output <= (others => '0'); input1_buf <= (others => '0'); part0 <= (others => '0'); part1 <= (others => '0'); part2 <= (others => '0'); part3 <= (others => '0'); part4 <= (others => '0'); part5 <= (others => '0'); part6 <= (others => '0'); part7 <= (others => '0'); elsif rising_edge(CLK) then input1_buf <= input1(7)&input1(7)&input1(7)&input1(7)&input1(7)&input1(7)&input1(7)&input1(7)&signed(input1); if (input2(0)='1') then part0 <= -(input1_buf); else part0 <= (others => '0'); end if; if (input2(1)='1') then if (input2(0)='1') then part1 <= (others => '0'); else part1 <= -(input1_buf); end if; else if (input2(0)='1') then part1 <= input1_buf; else part1 <= (others => '0'); end if; end if; if (input2(2)='1') then if (input2(1)='1') then part2 <= (others => '0'); else part2 <= -(input1_buf); end if; else if (input2(1)='1') then part2 <= input1_buf; else part2 <= (others => '0'); end if; end if; if (input2(3)='1') then if (input2(2)='1') then part3 <= (others => '0'); else part3 <= -(input1_buf); end if; else if (input2(2)='1') then part3 <= input1_buf; else part3 <= (others => '0'); end if; end if; if (input2(4)='1') then if (input2(3)='1') then part4 <= (others => '0'); else part4 <= -(input1_buf); end if; else if (input2(3)='1') then part4 <= input1_buf; else part4 <= (others => '0'); end if; end if; if (input2(5)='1') then if (input2(4)='1') then part5 <= (others => '0'); else part5 <= -(input1_buf); end if; else if (input2(4)='1') then part5 <= input1_buf; else part5 <= (others => '0'); end if; end if; if (input2(6)='1') then if (input2(5)='1') then part6 <= (others => '0'); else part6 <= -(input1_buf); end if; else if (input2(5)='1') then part6 <= input1_buf; else part6 <= (others => '0'); end if; end if; if (input2(7)='1') then if (input2(6)='1') then part7 <= (others => '0'); else part7 <= -(input1_buf); end if; else if (input2(6)='1') then part7 <= input1_buf; else part7 <= (others => '0'); end if; end if; out_temp <= part0+ (part1(14 downto 0)&'0')+ (part2(13 downto 0)&"00")+ (part3(12 downto 0)&"000")+ (part4(11 downto 0)&"0000")+ (part5(10 downto 0)&"00000")+ (part6(9 downto 0)&"000000")+ (part7(8 downto 0)&"0000000"); output <= out_temp(15 downto 8); end if; end process; END behavior;