ECDSA (Elliptic Curve Digital Signature Algorithm)

1.0 Digital Signatures

Digital signatures are a cryptographic tool to sign messages and verify message signatures in order to provide proof of authenticity for digital messages or electronic documents. Digital signatures provide:

    • Message authentication - a proof that certain known sender (secret key owner) have created and signed the message.
    • Мessage integrity - a proof that the message was not altered after the signing. .
    • Non-repudiation - the signer cannot deny the signing of the document after the signature is once created. .

Digital signatures are widely used today in the business and in the financial industry, e.g. for authorizing bank payments (money transfer), for exchange of signed electronic documents, for signing transactions in the public blockchain systems (e.g. transfer of coins, tokens or other digital assets), for signing digital contracts and in many other scenarios.

1.1 Sign Messages and Verify Signatures: How It Works?

Digital signature schemes typically use a public-key cryptosystem (such as RSA or ECC) and use a public / private key pairs. A message is signed by a private key and the signature is verified by the corresponding public key:

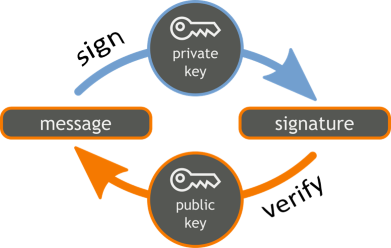
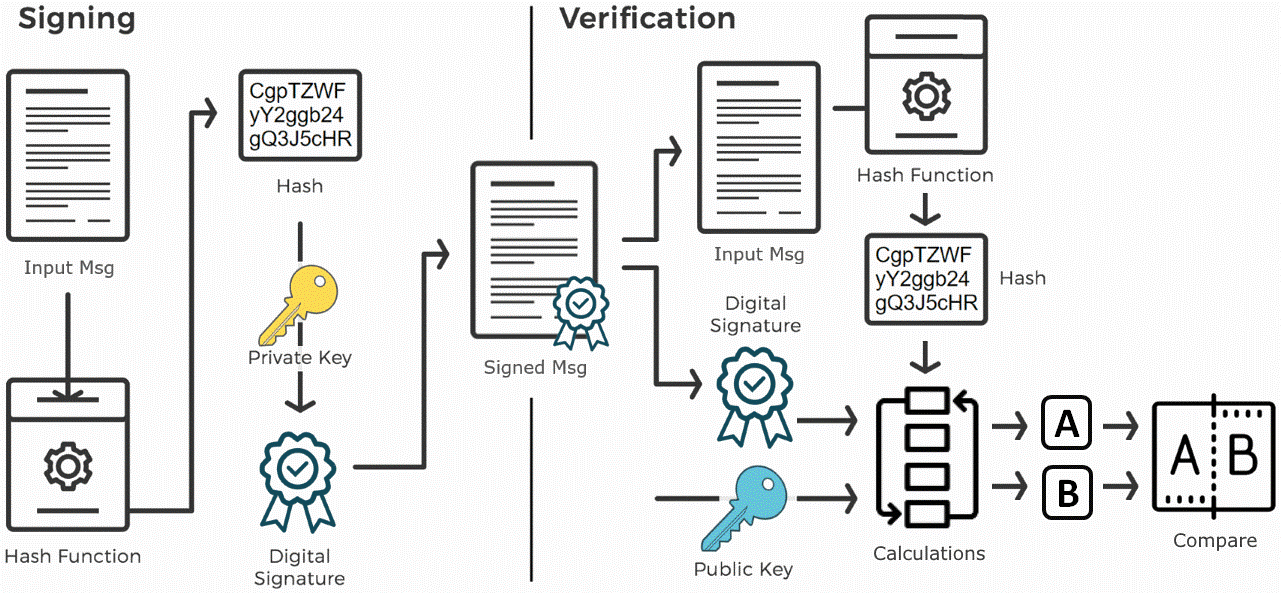
Messages are signed by the sender using a private key (signing key). Typically the input message is hashed and then the signature is calculated by the signing algorithm. Most signature algorithms perform some calculation with the message hash + the signing key in a way that the result cannot be calculated without the signing key. The result from message signing is the digital signature (one or more integers):

Message signatures are verified by the corresponding public key (verification key). Typically the signed message is hashed and some calculation is performed by the signature algorithm using the message hash + the public key. The result from signing is a boolean value (valid or invalid signature):

A message signature mathematically guarantees that certain message was signed by certain (secret) private key, which corresponds to certain (non-secret) public key. After a message is signed, the message and the signature cannot be modified and thus message authentication and integrity is guaranteed. Anyone, who knows the public key of the message signer, can verify the signature. Аfter signing the signature author cannot reject the act of signing (this is known as non-repudiation). Most signature schemes work like it is shown at the following diagram:

Digital Signature using Elliptic Curve Digital Signature Algorithm

The ECDSA key-pair consists of:

• • private key (integer): privKey
• • public key (EC point): pubKey = privKey * G

The private key is generated as a random integer in the range [0...n-1]. The public key pubKey is a point on the elliptic curve, calculated by the EC point multiplication: pubKey = privKey * G (the private key, multiplied by the generator point G ). The public key EC point {x, y} can be compressed to just one of the coordinates + 1 bit (parity). For the secp256k1 curve, the private key is 256-bit integer (32 bytes) and the compressed public key is 257-bit integer (~ 33 bytes).

Suppose two patners(usually Alice and Bob, lol) wants to communicate and Alice wants to send Bob a message. Alice has to first sign the message to confirm its Genuity.

So how will Alice sign the file/message ?

z = Hash(M), where M is the message wants to send and z is the hash of the message.
Now that we have the hash z, we can take a look at the steps, that Alice’s signing algorithm will run through:

• 1. Choose a large integer number k from the set of numbers 0,…,n-1. To understand the algorithm, it is not necessary to understand, under which conditions the number n is chosen. Together with the point G being used to get the public key, another point E on the curve is being calculated.
• E= kG.
• 2. The calculated point H has a x- and a y-coordinate, E= (x_e ,y_e). Using the x-coordinate of the point, the first part of the signature will be: .
• r = x_e mod n .
• The abbreviation mod means, that modular arithmetics is applied. Don’t worry! It’s not complicated at all. It just means division with rest. If you take a number modulo another number, for example 7 mod 4, the result will be the rest from the division. Dividing 7 by 4 results in a rest of 3, so .
• 7 mod 4 = 3. .
• 3. Is the result for r equals zero, the algorithm goes back to step one and starts over with a new number k. .
• 4. Now the second part of the signature will be calculated. Therefore, ECDSA requires the Hash z of the message, Alice intends to send, her private key and the lately calculated first part of the signature r. The second part s of the signature has the following form: .
• s = k^-1 ⋅ (z+r ⋅ d_a ) mod n.
• 5. If s equals zero, the algorithm has to jump back to the first step and start all over again. .

Going through these steps, will eventually give you a pair of numbers
(r,s) -this is the desired signature. Now that we know how a signature is created, the next part of interest will be, how it can be verified by the recipient of the message, i.e. Bob.

Verifying the signature

Alice sent her message out and Bob received it together with the signature attached. Now he wants to know if the message, he received, is indeed coming from Alice. All the information he got is just the signature (r,s) itself, the message(M) and Alice’s public key P_a. A way has to be found, that he can verify the signature using only those pieces of information. To do so, Bob’s Verifying Algorithm needs to calculate the point E and has to prove, that x_e fulfills the following requirement:

x_e mod n = r

Concerning the point E, this equation holds:

E = k ⋅ G

The one problem is, that Bob does not know what k is. But there is a way! Let’s take the equation from the fourth step of the signing algorithm:

s = k^-1 ⋅ (z+r ⋅ d_a ) mod n

We can reformulate in way, such that we get an expression for the number k:

k = s^-1 ⋅ (z+r ⋅ d_a ) mod n

Taking this expression for k, we can rewrite the equation for calculating the point E:

E = k ⋅ G = s^-1 ⋅ (z+r ⋅ d_a ) ⋅G mod n

Now we are going to do a little maths. We multiply out the brackets first:

E = (s^-1 ⋅ z ⋅ G) mod n + (s^-1 ⋅ r ⋅ d_a ⋅ G) mod n

Remembering the definition of the public key shown in the introduction to this article

P_a = d_a ⋅ G

we can replace the multiplication of the private key by the point G with Alice’s public key. Thus, the point E can now be calculated using only the information of the Hash z of the message, Alice’s public key and the signature:

E = (s^-1 ⋅ z ⋅ G) mod n + (s^-1 ⋅ r ⋅ P_a ) mod n

Now that we have derived a way to verify a signature, it’s time to summarize the single steps of the Verifying Algorithm:

• 1. Take the signature (r,s) and calculate the multiplicative inverse s^-1. Using the truncated Hash z of the message, calculate the number A₁ = s^-1⋅ z
• 2. Calculate the number A₂ = s^-1 ⋅ r .
• 3. Evaluate the point E = A₁ ⋅ G + A₂ ⋅ P_a
• 4. Take the x- coordinate x_e of the point E and check whether the following condition holds:
  x_e mod n = r
• If this condition holds, the signature is correct!

So The ECDSA sign / verify process works as follows:

• • The ECDSA signing algorithm computes a message hash, then generates a random integer k and computes the signature (a pair of integers {r, s}), where r is computed from k and s is computed using the message hash + the private key + the random number k. Due to the randomness, the signature is non-deterministic.
• • The ECDSA signature verification algorithm involves computations, based on the message hash + the public key + the signature {r, s}.

Diffie Hellman Using ECC

Now that we know all the ECC parameters, let’s walk through the implementation of ECC using the Diffie Hellman key exchange protocol. Imagine that Alice wants to establish a secure connection with Bob and she chooses ECC Diffie Hellman as the mechanism to exchange encryption keys. First, Alice will choose a random number between 1 and n-1. We will call it ⍺. At the same time, Bob is choosing a random number between 1 and n-1 as well. We’ll call Bob’s value β. Now we have:

⍺: randomly chosen number between 1 and n-1. This is the private key for Alice

β: randomly chosen number between 1 and n-1. This is the private key for Bob

Next, Bob computes the value B = β (G). Bob can compute this value because he knows the values for β and G. At the same time, Alice computes A = ⍺ (G). Alice can compute this value because she knows the values for ⍺ and G.

Next, Bob sends Alice the point on the curve (x_B, y_B), and Alice sends Bob the point on the curve (x_A, y_A). These two points on the curve are the public key values for Bob and Alice. Still, neither person knows the other person’s private key value (⍺ or β). They only know A and B (public keys) because they were sent those respective points on the curve. A malicious eavesdropper would have all the values except for ⍺ and β (the private keys). While a man in the middle could verify that A and B are points on the given elliptic curve, he would not know how many hops the points are from the initial generator point (G). He would need the value for ⍺ or β to know the number of hops. Again, this is the foundation of the Elliptic Curve Discrete Logarithm Problem.

Next, Bob and Alice then compute the value P by multiplying their respective private key value by the value received by the other person. So,

Bob computes: P = β * A or, substituting ⍺ (G) for A, you get P = β * ⍺ * G

Alice computes: P = ⍺ * B or, substituting β (G) for B, you get P = ⍺ * β * G

Now, Bob and Alice both have the point P that they can use as their symmetric key encryption value!

A Working Example…

Let’s take all this goodness and actually work through an example with real numbers! Keep in mind, the values for this curve and all the other associated parameters have been worked out in advance. This curve uses very small numbers for p and n, so you wouldn’t want to use this specific curve in real life.

Here are the values for our ECC cryptosystem using the Diffie Hellman key exchange protocol:

Curve: y² = x³ + 2x + 2 (mod 17)

• p: 17 (notice this is a prime number, so this is considered a “prime” curve)
• a: 2
• b: 2
• G: (5,1)
• n: 19

To find n, you Point Double/Point Add starting from G until you reach a point at infinity. That is, the operations continue until the resultant line is vertical. In this case, n = 19. Here are the first few operations for this particular curve; starting at the Generator Point (5,1):

2G = G + G = (6,3) Note: this point is found using Point Doubling

3G = 2G + G = (10,6) Note: the remaining points are found using Point Addition

4G = 3G + G = (3,1)

…

19G = ?

h = 1 (which is the ideal value for h)

Now we are ready to start computing values for ⍺ and β. Alice picks a value for ⍺. The value for ⍺ must be between 1 and n-1 (18).
⍺ = 3
Next, Alice computes the value for A:
A = ⍺ * G = 3G; A = (10,6)

Note: compare this point 3G to the 3G point listed above in the calculations for “n”. This is how you know what point is represented by 3G.

Notice that the value for A is not a single number. Rather, it is the point on the curve represented by Point Doubling/Point Addition operations conducted ⍺ times. .

Bob picks a value for β. The value for β must be between 1 and n-1 (18).

β = 9.

B = β * G = 9G.

B = (7,6) .

They share the values A and B with each other and are then ready to both compute the value for P. .

Bob computes
P = β * A = β * 3G = 9 * 3G = 27G.
Because the order of the curve (n) is 19, 27G reduces to 8G. If the value for P results in a number higher than the order of the curve, you use the modulo operation to find the resulting value. In this example, 27 mod 19 = 8. So, 27G becomes 8G because 27 is larger than 19. .

Alice computes
P = ⍺ * B = ⍺ * 9G = 3 * 9G = 27G.

Alice uses the same logic as Bob in reducing 27G to 8G.
So, P = 8G = (13,7)

Now, Bob and Alice both have the point (13,7) as their shared secret, and the man in the middle has no idea what the value for P is. They don’t need to use both the x-value and the y-value, so they can just throw away one of the values (let’s say they throw away the y-value). Now, they have the value 13 as a shared secret and they can use this to encrypt all further communication.