CORDIC stands for Coordinate Rotation Digital Computer. It calculates the value of trigonometric functions like sine, cosine, magnitude and phase to any desired precision. It can also calculate hyperbolic functions (such as sinh, cosh and tanh). The CORDIC algorithm does not use calculus based methods such as polynomial or rational function approximation.
In a digital system, The standard method of rotating a point (x1, y1) by an angle θ in the xyplane to a point (x2, y2) is given by :

X2 = x1cosθ - y1sinθ
Y2= x1sinθ + y1cosθ
We call this equation 1.
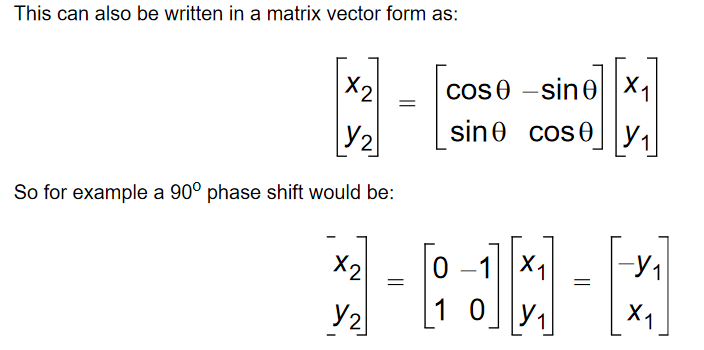
By eliminating cosθ:
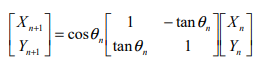
We call this equation 2.It can be seen that cosθ is more of a scaling factor. during our implementation in OFDM, an arbitrary gain will be used for multiplication rather than cosθ. Since we are implementing in a digital system multiplications and divisions can be reduced further by introducing θ, be to a unit step in base 2 , so divisions and mutliplications can be represented as just addition and substraction.
Additional multipliers can be eliminated by selecting the angle steps such that the tangent of a step is a power of 2. Multiplying or dividing by a power of 2 can be implemented using a simple shift operation. The angle for each step is given by :
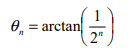
This results in the following equation for tanθ
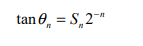
S, represents a sign {-1;+1}
combining this new value of tanθ with equation 2, yields equation 3:
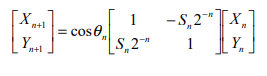
And the final cordic equation is represented as:

We call this equation 3
At this point a new variable called ‘Z’ is introduced. Z represents the part of the angle θ
which has not been rotated yet. since it is an interation If we add the computation for X and Y we get the program-like style for the CORDIC
core.
For n=0 to [inf]
If (Z(n) >= 0) then
X(n + 1) := X(n) – (Yn/2^n);
Y(n + 1) := Y(n) + (Xn/2^n);
Z(n + 1) := Z(n) – atan(1/2^n);
Else
X(n + 1) := X(n) + (Yn/2^n);
Y(n + 1) := Y(n) – (Xn/2^n);
Z(n + 1) := Z(n) + atan(1/2^n);
End if;
End for;
Note:
The code above represents one rotation or iteration, we would perform multiples iterations to get a particular sine or cosine value, that is
why Z was introduced to store the angle at a particular iteration.
Multiple iterations are performed since one iteration cannot lead us to the exact angle we are looking for, since there is no lookup table.
from the code above, Z(n) >= 0 represents when S=+1, and vice versa.
We can calculate the sine, and cosine of angles from equation 1, by setting Y to zero and X to a constant gain.
An example is given below:
Example:
Calculate sine and cosine of 30degrees.
First the angle has to be calculated into binary using a scale:
360o = 216 since we would be using a 16-bit input
30o = ????
We cross multiply
(30 * 216) /360 = 5461 (dec) = 1555 (hex)
Converting to binary = 1 0101 0101 0101
so the above result is what we input to the angle, while setting Y = 0, and X= a constant gain
In mathematics further calculations are used to derive the constant gain as 0.607.......
But for the sake of OFDM or FFT in FPGA an arbitrary gain can be used to scale it to a given threshold
without affecting the sine and cosine outputs as seen from the earlier derivations above:
We already have a table of arctan i.e tan-1θ. Ranging from
θ =
[1/20 , 1/21 , 1/22 , 1/23 , 1/24 , 1/25 , 1/26 , 1/27 ,
……… 1/2n-1 , ] n= no of iterations
In degrees it is equal to
[45o, 26.565o, 14.036o, 7.125o, 3.576o, 1.790o, 0.8950o ……….]
Starting from θ = 0o
cosθ = 1 ….. X=1
Sinθ = 1 ….. Y=0
Now we perform the first iteration
Rotating from 0o to 45oi.e (arctan 1/20)
Substituting X=1, Y=0 ( from above. ), S = +1 (since it is a positive rotation) , 2-n =1 where n=0, ….all into eqn3
X1 = X0 - (+1)Y0 /20=1 - 0/1 = 1
Y1 = (+1)X0/20 +Y0 =1/1 + 0 = 1
Performing the second iteration
Since 45o is greater than 30o next rotation will be negative.
Rotating 26.565oi.e (arctan 1/21) from 45o
45 – 26.565 = 18.435o
Substituting X=1, Y=1 ( from above. ), S = -1 (since it is a negative rotation) , 2-n =1/2, where n=1….all into eqn3
X2 = X1 - (-1)Y1 /21=1 + 1/2 = 1.5
Y2 = (-1)X1/21 +Y1 =-1/2 + 1 = 0.5
Performing the Third iteration
Since 18.435o is less than 30o, next rotation will be positive
Rotating 14.036oi.e (arctan 1/22) from 18.435o
18.435o + 14.036o = 32.4710o
Substituting X=1.5, Y=0.5 ( from above. ), S = +1 (since it is a positive rotation) , 2-n =1/4, where n=2….all into eqn3
X3 = X2 - (+1)Y2 /22=1.5 - 0.5/4 = 1.375
Y3 = (+1)X2/22 +Y2 =1.5/4 + 0.5 = 0.875
Performing the fourth iteration
Since 32.4710o is greater than 30o, next rotation will be negative
Rotating 7.125oi.e (arctan 1/23) from 32.4710o
32.4710o - 7.125o = 25.346o
Substituting X=1.375, Y=0.875 ( from above. ), S = -1 (since it is a negative rotation) , 2-n =1/8, where n=3….all into eqn3
X4 = X3 - (-1)Y3 /23=1.375 + 0.875/8 = 1.484375
Y4 = (-1)X3/23 +Y3 =-1.375/8 + 0.875= 0.703125
Performing the fifth iteration
Since 25.346o is less than 30o, next rotation will be positive
Rotating 3.576oi.e (arctan 1/24) from 25.346o
25.346o + 3.576o = 28.922o
Substituting X=1.484375, Y=0.703125 ( from above. ), S = +1 (since it is a positive rotation) , 2-n =1/16, where n=4….all into eqn3
X5 = X4 - (+1)Y4 /24=1.484375 - 0.703125/16 = 1.440429
Y5 = (+1)X4/24 +Y4 =1.484375/16 + 0.703125= 0.795898
Performing the sixth iteration
Since 28.922o is less than 30o, next rotation will be positive
Rotating 1.790oi.e (arctan 1/25) from 28.922o
28.922o + 1.790o = 30.712o
Substituting X=1.440429, Y=0.795898 (from above. ), S = +1 (since it is a positive rotation) , 2-n =1/32, where n=5….all into eqn3
X6 = X5 - (+1)Y5 /25=1.440429 - 0.795898/32 = 1.4155571875
Y6 = (+1)X5/25 +Y5 =1.440429/32 + 0.795898 = 0.840911406
you can either stop here, continue till you get exactly 30degrees or go as long as your iteration requires. In designing digital circuit i.e., a Verilog or VHDL script for the algorithm, if your desired input bit is 16, then you have to keep the iteration for 16 times irrespective of if you get the exact value. Usually before up to 16 iterations you must have landed on the exact required figure.
In the design the Z input usually hold your desired degree, and instead of counting from zero up to the required degree. We actually reduce it down to zero from the angle. The iterations drive the X and Y output between negative and positive values, till it finally reaches zero.
After that we have to just multiply by the aggregate constant 0.607253. i.e
X = 0.607253 * 1.4155571875 = 0.8596013
Y = 0.607253 * 0.840911406 = 0.510645 approx 0.5
It is a mathematical constant, but in digital design , it can be arbitrary constant gain depending on the designers choice and type of signal you are
dealing with. Its just a digital amplifier.
Now, The outputs represent values in the –1 to +1 range.
The core will output .
Sin : 16380(dec) = 3FFC(hex)
Cos : 28381(dec) = 6EDD(hex)
The results can be derived as follows:
215 = 1;
Sin30 = 16380 = ????
Cos30 = 28381 = ?????
Sin30 = (16380 * 1) / 215 = 0.499999
Cos30 = (28381 * 1) / 215 = 0.8661
Now, this is the end of this lecture on cordic , the aim of the course is to design an OFDM unit in FPGA. Next tutorial would concentrate on FFT(fast fourier transform) unit. all these would be sub units in the OFDM circuit.
The verilog code for the cordic algorithm is given below.
library ieee; use ieee.std_logic_1164.all; use ieee.std_logic_arith.all; entity p2r_CordicPipe is generic( WIDTH : natural := 16; PIPEID : natural := 1 ); port( clk : in std_logic; ena : in std_logic; Xi : in signed(WIDTH -1 downto 0); Yi : in signed(WIDTH -1 downto 0); Zi : in signed(19 downto 0); Xo : out signed(WIDTH -1 downto 0); Yo : out signed(WIDTH -1 downto 0); Zo : out signed(19 downto 0) ); end entity p2r_CordicPipe; architecture dataflow of p2r_CordicPipe is -- -- functions -- -- Function CATAN (constante arc-tangent). -- This is a lookup table containing pre-calculated arc-tangents. -- 'n' is the number of the pipe, returned is a 20bit arc-tangent value. -- The numbers are calculated as follows: Z(n) = atan(1/2^n) -- examples: -- 20bit values => 2^20 = 2pi(rad) -- 1(rad) = 2^20/2pi = 166886.053.... -- n:0, atan(1/1) = 0.7853...(rad) -- 0.7853... * 166886.053... = 131072(dec) = 20000(hex) -- n:1, atan(1/2) = 0.4636...(rad) -- 0.4636... * 166886.053... = 77376.32(dec) = 12E40(hex) -- n:2, atan(1/4) = 0.2449...(rad) -- 0.2449... * 166886.053... = 40883.52(dec) = 9FB3(hex) -- n:3, atan(1/8) = 0.1243...(rad) -- 0.1243... * 166886.053... = 20753.11(dec) = 5111(hex) -- function CATAN(n :natural) return integer is variable result :integer; begin case n is when 0 => result := 16#020000#; when 1 => result := 16#012E40#; when 2 => result := 16#09FB4#; when 3 => result := 16#05111#; when 4 => result := 16#028B1#; when 5 => result := 16#0145D#; when 6 => result := 16#0A2F#; when 7 => result := 16#0518#; when 8 => result := 16#028C#; when 9 => result := 16#0146#; when 10 => result := 16#0A3#; when 11 => result := 16#051#; when 12 => result := 16#029#; when 13 => result := 16#014#; when 14 => result := 16#0A#; when 15 => result := 16#05#; when 16 => result := 16#03#; when 17 => result := 16#01#; when others => result := 16#0#; end case; return result; end CATAN; -- function Delta is actually an arithmatic shift right -- This strange construction is needed for compatibility with Xilinx WebPack function Delta(Arg : signed; Cnt : natural) return signed is variable tmp : signed(Arg'range); constant lo : integer := Arg'high -cnt +1; begin for n in Arg'high downto lo loop tmp(n) := Arg(Arg'high); end loop; for n in Arg'high -cnt downto 0 loop tmp(n) := Arg(n +cnt); end loop; return tmp; end function Delta; function AddSub(dataa, datab : in signed; add_sub : in std_logic) return signed is begin if (add_sub = '1') then return dataa + datab; else return dataa - datab; end if; end; -- -- ARCHITECTURE BODY -- signal dX, Xresult : signed(WIDTH -1 downto 0); signal dY, Yresult : signed(WIDTH -1 downto 0); signal atan, Zresult : signed(19 downto 0); signal Zneg, Zpos : std_logic; begin dX <= Delta(Xi, PIPEID); dY <= Delta(Yi, PIPEID); atan <= conv_signed( catan(PIPEID), 20); -- generate adder structures Zneg <= Zi(19); Zpos <= not Zi(19); -- xadd Xresult <= AddSub(Xi, dY, Zneg); -- yadd Yresult <= AddSub(Yi, dX, Zpos); -- zadd Zresult <= AddSub(Zi, atan, Zneg); gen_regs: process(clk) begin if(clk'event and clk='1') then if (ena = '1') then Xo <= Xresult; Yo <= Yresult; Zo <= Zresult; end if; end if; end process; end architecture dataflow;
library ieee; use ieee.std_logic_1164.all; use ieee.std_logic_arith.all; entity p2r_cordic is generic( PIPELINE : integer := 15; WIDTH : integer := 16); port( clk : in std_logic; ena : in std_logic; Xi : in signed(WIDTH -1 downto 0); Yi : in signed(WIDTH -1 downto 0) := (others => '0'); Zi : in signed(19 downto 0); Xo : out signed(WIDTH -1 downto 0); Yo : out signed(WIDTH -1 downto 0) ); end entity p2r_Cordic; architecture dataflow of p2r_cordic is -- -- TYPE defenitions -- type XYVector is array(PIPELINE downto 0) of signed(WIDTH -1 downto 0); type ZVector is array(PIPELINE downto 0) of signed(19 downto 0); -- -- COMPONENT declarations -- component p2r_CordicPipe generic( WIDTH : natural := 16; PIPEID : natural := 1 ); port( clk : in std_logic; ena : in std_logic; Xi : in signed(WIDTH -1 downto 0); Yi : in signed(WIDTH -1 downto 0); Zi : in signed(19 downto 0); Xo : out signed(WIDTH -1 downto 0); Yo : out signed(WIDTH -1 downto 0); Zo : out signed(19 downto 0) ); end component p2r_CordicPipe; -- -- SIGNALS -- signal X, Y : XYVector; signal Z : ZVector; -- -- ACHITECTURE BODY -- begin -- fill first nodes -- fill X X(0) <= Xi; -- fill Y Y(0) <= Yi; -- fill Z Z(0)(19 downto 0) <= Zi; -- modified by zhaom --Z(0)(3 downto 0) <= (others => '0'); -- modified by zhaom -- -- generate pipeline -- gen_pipe: for n in 1 to PIPELINE generate Pipe: p2r_CordicPipe generic map(WIDTH => WIDTH, PIPEID => n -1) port map ( clk, ena, X(n-1), Y(n-1), Z(n-1), X(n), Y(n), Z(n) ); end generate gen_pipe; -- -- assign outputs -- Xo <= X(PIPELINE); Yo <= Y(PIPELINE); end dataflow;
library ieee; use ieee.std_logic_1164.all; use ieee.std_logic_arith.all; use ieee.std_logic_signed.all; entity sc_corproc is generic ( WIDTH : Natural; STAGE : Natural ); port( clk : in std_logic; ena : in std_logic; Xin : in signed(WIDTH+1 downto 0); Yin : in signed(WIDTH+1 downto 0); Ain : in signed(2*STAGE-3 downto 0 ); sin : out signed(WIDTH+3 downto 0); cos : out signed(WIDTH+3 downto 0) ); end entity sc_corproc; architecture dataflow of sc_corproc is constant PipeLength : natural := 2*STAGE+2; component p2r_cordic is generic( PIPELINE : integer := 15; WIDTH : integer := 16); port( clk : in std_logic; ena : in std_logic; Xi : in signed(WIDTH -1 downto 0); Yi : in signed(WIDTH -1 downto 0) := (others => '0'); Zi : in signed(19 downto 0); Xo : out signed(WIDTH -1 downto 0); Yo : out signed(WIDTH -1 downto 0) ); end component p2r_cordic; signal phase:signed( 19 downto 0 ); signal Xi,Yi:signed( WIDTH+7 downto 0 ); signal Xo,Yo:signed( WIDTH+7 downto 0 ); signal zeros:signed( 19-STAGE*2 downto 0 ); begin Xi<= Xin(WIDTH+1)&Xin&"00000"; Yi<= Yin(WIDTH+1)&Yin&"00000"; zeros<=(others=>'0'); phase<="00"&Ain&zeros; cos<=Xo(WIDTH+7)&Xo( WIDTH+7 downto 5 ); sin<=Yo(WIDTH+7)&Yo( WIDTH+7 downto 5 ); u1: p2r_cordic generic map(PIPELINE => PipeLength, WIDTH => WIDTH+8) port map(clk => clk, ena => ena, Xi => Xi, Yi=>Yi,Zi => phase, Xo => Xo, Yo => Yo); end architecture dataflow;