Amplitude Shift Keying (ASK) and On-Off Keying (OOK) Amplitude
Shift Keying is a form of amplitude modulation that represents digital data as shifts in the amplitude of a carrier wave: for example, small amplitude for a 0-bit,
and larger amplitude for a 1-bit. We have seen what an ASK signal looks like in a previous chapter, repeated below.
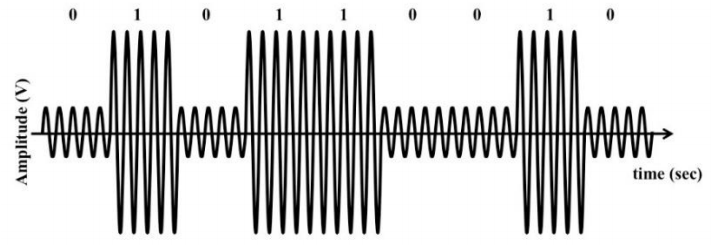
The simplest digital modulation scheme is a form of ASK called On-Off keying (OOK). This is analogous to flashing light communication. In OOK, a carrier is transmitted for a 1-bit and nothing is transmitted for a 0-bit; this is the same as saying that the smaller ASK amplitude is 0.
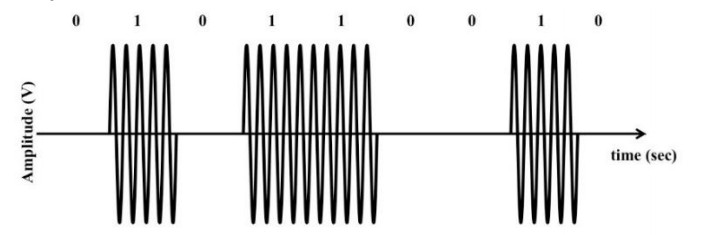
Note that in all forms of ASK, the frequency and phase of the carrier are the same for both symbols; it is the amplitude that changes.
FREQUENCY-SHIFT KEYING FSK
is a form of constant-amplitude angle modulation similar to standard frequency modulation (FM) except the modulating signal is a binary signal that
varies between two discrete voltage levels rather than a continuously changing analog waveform. Frequency Shift Keying (FSK) Frequency-shift keying (FSK) is a frequency
modulation scheme in which digital information is transmitted through discrete frequency changes (shifts) of a carrier wave. The simplest form of FSK is Binary FSK (BFSK),
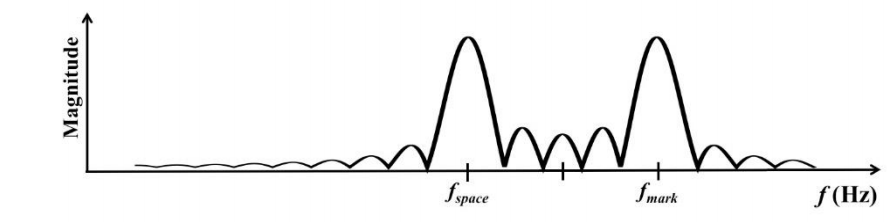
in which a carrier’s frequency is shifted to a low frequency or a high frequency to transmit 0s and 1s. The plot below shows a sample FSK signal along with the associated bits.

FSK was used “back in the day” with dial-up modems to connect your home computer to your Internet service provider over your analog phone. With a modem, a 0-bit was represented with a lower frequency carrier of 1070 Hz and a 1-bit was represented with a higher carrier frequency of 1270 Hz. The lower frequency, binary 0, was called the “space” frequency while the higher frequency, binary 1, was called the “mark” frequency. The terms mark/space were a throwback to the days of Morse code or flashing light communications. In the frequency domain, we use two carrier frequencies and consider FSK to be two different digital transmissions, one at the mark frequency (the higher frequency) and one at the space frequency (lower frequency). The resulting FSK frequency plot would look like the following. This figure is two copies of the frequency plot on the previous page, one centered at fmark and one centered at fspace.
To determine the bandwidth for FSK modulation, we take a closer look at the frequency spectrum around the mark and space frequencies. We use the null-bandwidth definition to compute the bandwidth as shown below.
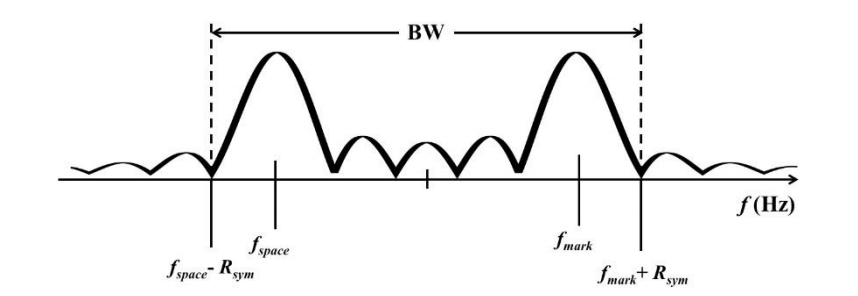
In the figure, the bandwidth effectively runs from the first null to the left of fspace to the first null to the right of fmark. Mathematically, we can compute the FSK bandwidth as:
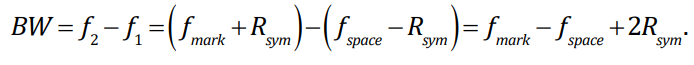
Or, for FSK, since the symbol rate is equal to the bit rate, we could also use the equation:
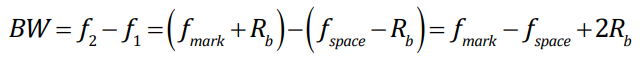
Binary Phase Shift Keying (BPSK)
The first modulation considered is binary phase shift keying. In this scheme during every bit duration, denoted by T, one of two phases of the carrier is transmitted.
These two phases are 180 degrees apart. This makes these two waveforms antipodal. Any binary modulation where the two signals are antipodal gives the minimum error probability
(for fixed energy) over any other set of binary signals. The error probability can only be made smaller (for fixed energy per bit) by allowing more than two waveforms for
transmitting information.
We will begin our discussion of digital phase modulation with a review of the fundamentals of binary phase shift keying (BPSK), the simplest form of digital phase modulation. For BPSK, each symbol consists of a single bit. Accordingly, we must choose two distinct values of θ(t), one to represent 0, and one to represent 1. Since there are 2π radians per cycle of carrier, and since our symbols can only take on two distinct values, we can choose θ(t) as follows. Let θ1(t), the value of θ(t) that represents a one, be 0, and let θ0(t), the value of θ(t) that represents a zero, be π. Doing so, we obtain:
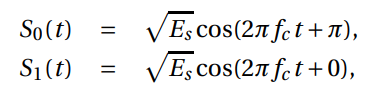
where √Es is the peak amplitude of the modulated sinusoidal carrier, S0(t) is the BPSK signal that represents a zero, and S1(t) is the BPSK signal that represents a one.
Phase Modulation Equals Amplitude Modulation
The expressions for S(t) given above clearly show BPSK as a form of phase modulation. However, since: cos(θ+π) = −cos(θ), we can rewrite S0(t)
and S1(t) as:
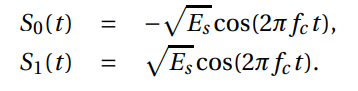
These expressions for S(t) show BPSK as a form of amplitude modulation, where A0(t) = −1 and A1(t) = +1. This begs the question: Is BPSK phase modulation or amplitude modulation? Both possibilities are correct, since the two are equivalent, as demonstrated by the trigonometric identity we used to convert between the two forms.
The modulation process is probably easier to understand when viewed from the perspective of amplitude modulation. For the example above, the carrier signal is
√Es cos(2πfc t),
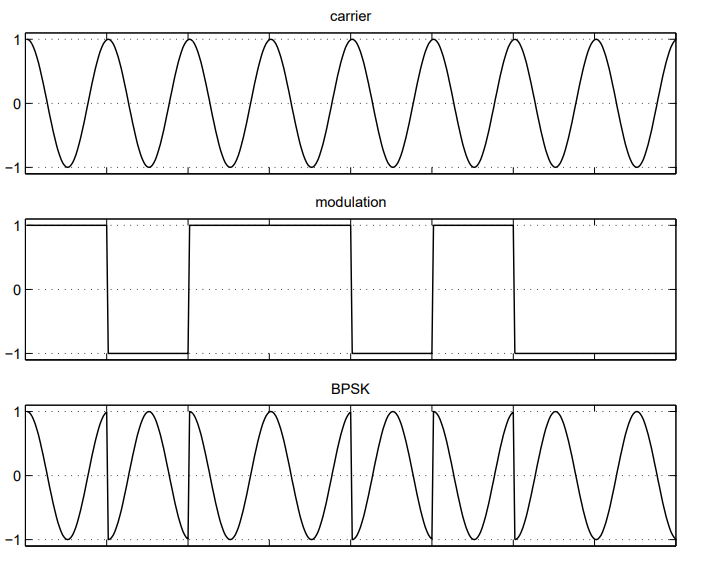
and the amplitude modulation is a square wave that has an amplitude of ±1 and a period of T , the duration of one symbol. The figure below illustrates how we create BPSK by multiplying a sinusoidal carrier by rectangular bit pulses.
An Alternate Choice of θ(t)
In the previous example, we chose θ0(t) = π and θ1(t) = 0. We could also chose θ0(t) = +π/ 2 and θ1(t) = −π /2 .
This results in:
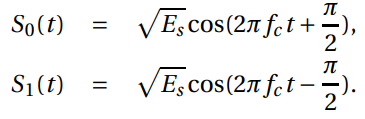
Using the identities sin(θ) = cos( π/ 2 − θ), cos(−θ) = cos(θ), and sin(−θ) = −sin(θ), we can re-write (3) as:
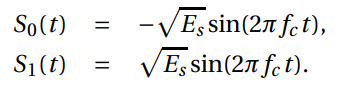
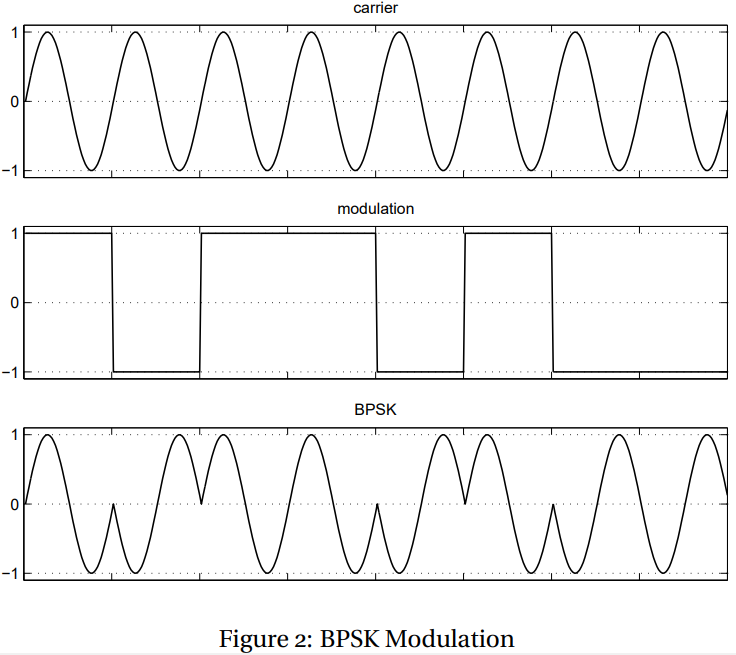
The result is once again a sinusoidal carrier multiplied by rectangular bit pulses, though the carrier is now sine instead of cosine, as shown above. Although this BPSK signal looks quite different from the one shown above, both represent the same bit pattern. The only difference is a carrier phase offset, caused by our choices of θ(t).
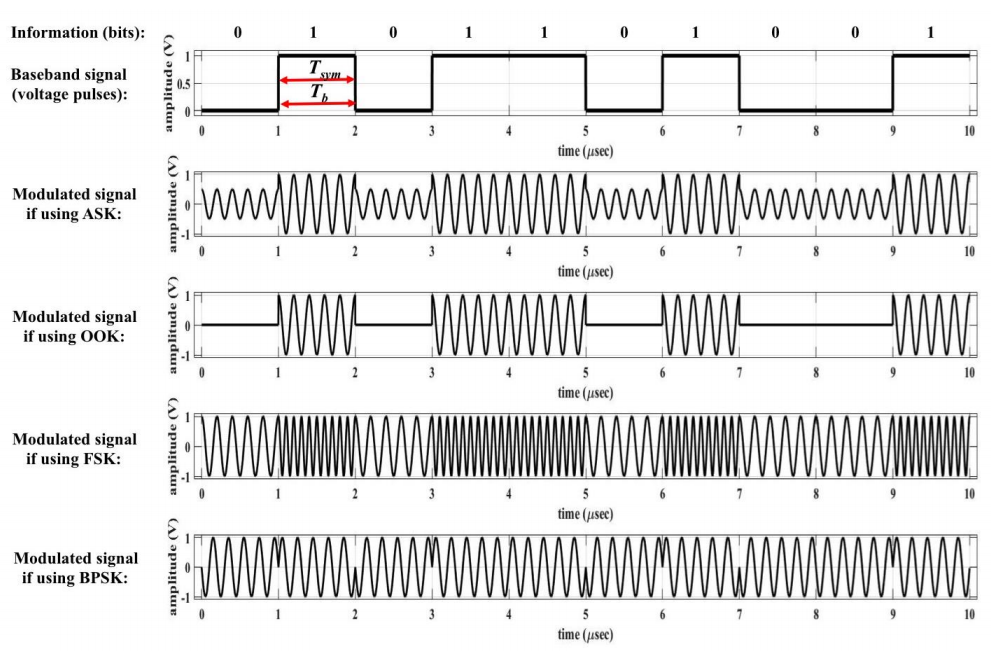
Let us now summarize the types of binary digital modulation that have been introduced so far. On a wire, the symbols take the form of voltage pulses, which are, for example, a high pulse for a 1-bit and a low (or no) pulse for a 0-bit. In FSK, ASK, OOK or BPSK, the symbols take the form of a high frequency carrier that has its frequency or amplitude or phase altered based on whether a 0-bit or a 1-bit is being transmitted. In binary modulation, the number of symbols that can be transmitted (M) is two (M = 2) and each symbol represents one bit of data (N = 1 bit per symbol). For binary modulation, the time duration of a bit is the same as the time duration of a symbol (Tb = Tsym). The following figure depicts the relationship between bits and symbols for voltage pulses (the baseband signal), and FSK, ASK, OOK and BPSK (the modulated signals)
Up to this point we have discussed binary digital modulation (M=2) with one bit per symbol (N=1), which means that at any time, only one of two possible symbols would be transmitted. But it is possible to have a modulation scheme with more than two symbols. This means that with each symbol, more than one bit is transmitted at a time. These types of modulation are referred to as M-ary digital modulation.